Disruptive Veränderungen (E-Mobilität, Smartphone etc.) und Epidemien ähneln sich im Verlauf. Zunächst gleicht ihr Verlauf einer exponentiellen Funktion (siehe Grafik).
Dann allerdings tritt – fast schlagartig – ein zweiter Mechanismus ein: die Kurve geht sehr schnell hoch (die konkrete Zeitdauer hängt von Faktoren wie Inkubationszeit, Abstand zwischen Infektion und Infektiösität ab), bis sie die Marke von 66,7% Durchseuchung erreicht hat.
Ab diesen Zeitpunkt ist die Wahrscheinlichkeit bei einer Infektion, deren erste Phase sich als exponentielle Funktion zur Basis 3 darstellen lässt, so, dass die Wahrscheinlichkeit, dass die drei folgenden „Kandidaten“ nur noch bei 33,3% liegt. Dies bedeutet, dass ab dann jeder neu Infizierte nur noch einen weiteren Menschen ansteckt und die Infektionswelle anfängt, auszulaufen.
Es entsteht die typische S-Kurve, die wir aus der Entwicklung disruptiver Prozesse in anderen Bereichen kennen. Mathematisch ist eine Pandemie oder Epedemie folglich möglicherweise als ein Sonderfall eines disruptiven Prozesses zu betrachten.
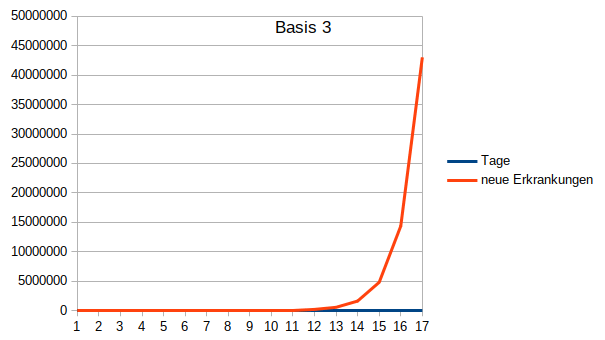
Eine Anmerkung zu der Zeichnung ist noch wichtig: Die hier dargestellte Verteilung geht von einer Umschlagsgeschwindigkeit von einem Tag aus. Das aktuell problematische Virus hat aber eine Umschlagsgeschwindigkeit von zwei Tagen, würde also nach 34 Tagen möglicherweise in den steilen Anstieg übergehen.

